Сейчас мы разберем положительные и отрицательные числа . Сначала дадим определения, введем обозначения, после чего приведем примеры положительных и отрицательных чисел. Также остановимся на смысловой нагрузке, которую несут в себе положительные и отрицательные числа.
Навигация по странице.
Положительные и отрицательные числа – определения и примеры
Дать определение положительных и отрицательных чисел нам поможет . Для удобства будем считать, что она расположена горизонтально и направлена слева направо.
Определение.
Числа, которые соответствуют точкам координатной прямой, лежащим правее начала отсчета, называют положительными .
Определение.
Числа, которые соответствуют точкам координатной прямой, лежащим левее начала отсчета называю отрицательными .
Число нуль, соответствующее началу отсчета, не является ни положительным, ни отрицательным числом.
Из определения отрицательных и положительных чисел следует, что множество всех отрицательных чисел представляет собой множество чисел, противоположных всем положительным числам (при необходимости смотрите статью противоположные числа). Следовательно, отрицательные числа всегда записываются со знаком минус.
Теперь, зная определения положительных и отрицательных чисел, мы с легкостью можем привести примеры положительных и отрицательных чисел . Примерами положительных чисел являются натуральные числа 5 , 792 и 101 330 , да и вообще любое натуральное число является положительным. Примерами положительных рациональных чисел являются числа , 4,67 и 0,(12)=0,121212... , а отрицательных – числа , −11 , −51,51 и −3,(3) . В качестве примеров положительных иррациональных чисел можно привести число пи, число e , и бесконечную непериодическую десятичную дробь 809,030030003… , а примерами отрицательных иррациональных чисел являются числа минус пи, минус e и число, равное . Следует отметить, что в последнем примере отнюдь не очевидно, что значение выражения является отрицательным числом. Чтобы это узнать наверняка, нужно получить значение этого выражения в виде десятичной дроби, а как это делается, мы расскажем в статье сравнение действительных чисел .
Иногда перед положительными числами записывается знак плюс, также как перед отрицательными числами записывается знак минус. В этих случаях следует знать, что +5=5
, ![]() и т.п. То есть, +5
и 5
и т.п. – это одно и то же число, но по-разному обозначенное. Более того, можно встретить определение положительных и отрицательных чисел, на основании знака плюс или минус.
и т.п. То есть, +5
и 5
и т.п. – это одно и то же число, но по-разному обозначенное. Более того, можно встретить определение положительных и отрицательных чисел, на основании знака плюс или минус.
Определение.
Числа со знаком плюс называют положительными , а со знаком минус – отрицательными .
Существует еще одно определение положительных и отрицательных чисел, основанное на сравнении чисел. Чтобы дать это определение, достаточно лишь вспомнить, что точка на координатной прямой, соответствующая большему числу, лежит правее точки, соответствующей меньшему числу.
Определение.
Положительные числа – это числа, которые больше нуля, а отрицательные числа – это числа, меньшие нуля.
Таким образом, нуль как бы отделяет положительные числа от отрицательных.
Конечно же, следует еще остановиться на правилах чтения положительных и отрицательных чисел. Если число записано со знаком + или −, то произносят название знака, после чего произносят число. Например, +8 читается как плюс восемь, а - как минус одна целая две пятых. Названия знаков + и − не склоняются по падежам. Примером правильного произношения является фраза «a равно минус трем» (не минусу трем).
Интерпретация положительных и отрицательных чисел
Мы уже достаточно долго описываем положительные и отрицательные числа. Однако неплохо было бы знать, какой смысл они несут в себе? Давайте разберемся с этим вопросом.
Положительные числа можно интерпретировать как приход, как прибавку, как увеличение какой-либо величины и тому подобное. Отрицательные числа, в свою очередь, означают строго противоположное – расход, недостаток, долг, уменьшение какой-либо величины и т.п. Разберемся с этим на примерах.
Можно сказать, что мы обладаем 3 предметами. Здесь положительное число 3 указывает количество находящихся у нас предметов. А как можно интерпретировать отрицательное число −3 ? Например, число −3 может означать, что мы должны кому-нибудь отдать 3 предмета, которых у нас даже нет в наличии. Аналогично можно сказать, что в кассе нам выдали 3,45 тысяч рублей. То есть, число 3,45 связано с нашим приходом. В свою очередь отрицательное число −3,45 будет указывать на уменьшение денег в кассе, выдавшей эти деньги нам. То есть, −3,45 – это расход. Еще пример: повышение температуры на 17,3 градуса можно описать положительным числом +17,3 , а понижение температуры на 2,4 можно описать с помощью отрицательного числа, как изменение температуры на −2,4 градуса.
Положительные и отрицательные числа часто используются для описания значений каких-либо величин в различных измерительных приборах. Самым доступным примером является прибор для измерения температур – термометр - со шкалой, на которой записаны и положительные и отрицательные числа. Часто отрицательные числа изображают синим цветом (он символизирует снег, лед, а при температуре ниже нуля градусов Цельсия начинает замерзать вода), а положительные числа записывают красным цветом (цвет огня, солнца, при температуре выше нуля градусов начинает таять лед). Запись положительных и отрицательных чисел красным и синим цветом используют и в других случаях, когда нужно особо выделить знак чисел.
Список литературы.
- Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
Мир чисел очень загадочен и интересен. Числа очень важны в нашем мире. Я хочу узнать как можно больше о происхождении чисел, об их значении в нашей жизни. Как их применять и какую роль они играют в нашей жизни?
В прошлом году на уроках математики мы начали изучать тему «Положительные и отрицательные числа». У меня возник вопрос, когда возникли отрицательные числа, в какой стране, какие ученые занимались этим вопросом. В Википедии я прочитал, что отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
В итоге я решил исследовать историю возникновения отрицательных чисел.
Целью данной работы является исследование истории возникновения отрицательных и положительных чисел.
Объект исследования - отрицательные числа и положительные числа
История положительных и отрицательных чисел
Люди долго не могли привыкнуть к отрицательным числам. Отрицательные числа казались им непонятными, ими не пользовались, просто не видели в них особого смысла. Эти числа появились значительно позже натуральных чисел и обыкновенных дробей.
Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н. э. и то, были известны лишь правила сложения и вычитания положительных и отрицательных чисел; правила умножения и деления не применялись.
Положительные количества в китайской математике называли «чен», отрицательные - «фу»; их изображали разными цветами: «чен» - красным, «фу» - черным. Это можно заметить в книге «Арифметика в девяти главах» (Автор Чжан Цань). Такой способ изображения использовался в Китае до середины XII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел - цифры, которые изображали отрицательные числа, перечеркивали черточкой наискось справа налево.
Лишь в VII в. индийские математики начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. Бхасхара прямо писал: "Люди не одобряют отвлеченных отрицательных чисел...". Вот как индийский математик Брахмагупта излагал правила сложения и вычитания: «имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество - долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму». «Сумма двух имуществ есть имущество».
(+х) + (+у) = +(х + у) (-х) + (-у) = - (х + у)
(-х) + (+у) = - (х - у) (-х) + (+у) = +(у - х)
0 - (-х) = +х 0 - (+х) = -х
Индийцы называли положительные числа «дхана» или «сва» (имущество), а отрицательные - «рина» или «кшайя» (долг). Индийские ученые, стараясь найти и в жизни образцы такого вычитания, пришли к толкованию его с точки зрения торговых расчетов. Если купец имеет 5000 р. и закупает товара на 3000 р., у него остается 5000 - 3000 = 2000, р. Если же он имеет 3000 р., а закупает на 5000 р., то он остается в долгу на 2000 р. В соответствии с этим считали, что здесь совершается вычитание 3000 - 5000, результатом же является число 2000 с точкой наверху, означающее «две тысячи долга». Толкование это носило искусственный характер, купец никогда не находил сумму долга вычитанием 3000 - 5000, а всегда выполнял вычитание 5000 - 3000.
Чуть позже в Древней Индии и Китае догадались вместо слов "долг в 10 юаней" писать просто "10 юаней", но рисовать эти иероглифы черной тушью. А знаков "+" и "-" в древности не было ни для чисел, ни для действий.
Греки тоже поначалу знаков не использовали. Древнегреческий ученый Диофант вообще не признавал отрицательные числа, и если при решении уравнения получался отрицательные корень, то он отбрасывал его как "недоступный". И Диофант старался так сформулировать задачи и составлять уравнения, чтобы избежать отрицательных корней, но вскоре Диофант Александрийский стал обозначать вычитание знаком.
Правила действий с положительными и отрицательными числами были предложены уже в III веке в Египте. Введение отрицательных величин впервые произошло у Диофанта. Он даже использовал специальный символ для них. В то же время Диофант употребляет такие обороты речи, как «Прибавим к обеим сторонам отрицательное», и даже формулирует правило знаков: «Отрицательное, умноженное на отрицательное, дает положительное, тогда как отрицательное, умноженное на положительное, дает отрицательное».
В Европе отрицательными числами начали пользоваться с XII-XIII вв., но до XVI в. большинство ученых считали их «ложными», «мнимыми» или «абсурдными», в отличие от положительных чисел - “истинных”. Положительные числа так же толковались как «имущество», а отрицательные - как «долг», «недостача». Даже знаменитый математик Блез Паскаль утверждал, что 0 − 4 = 0, так как ничто не может быть меньше, чем ничто. В Европе к идее отрицательного количества достаточно близко подошел в начале XIII столетия Леонардо Фибоначчи Пизанский. На состязании в решении задач с придворными математиками Фридриха II Леонардо Пизанскому было предложено решить задачу: требовалось найти капитал нескольких лиц. Фибоначчи получил отрицательное значение. "Этот случай, - сказал Фибоначчи, - невозможен, разве только принять, что один имел не капитал, а долг". Однако в явном виде отрицательные числа применил впервые в конце XV столетия французский математик Шюке. Автор рукописного трактата по арифметике и алгебре «Наука о числах в трёх частях». Символика Шюке приближается к современной.
Признанию отрицательных чисел способствовали работы французского математика, физика и философа Рене Декарта. Он предложил геометрическое истолкование положительных и отрицательных чисел - ввел координатную прямую. (1637 г.).
Положительные числа изображаются на числовой оси точками, лежащими вправо от начала 0, отрицательные - влево. Геометрическое истолкование положительных и отрицательных чисел способствовало к их признанию.
В 1544 году немецкий математик Михаил Штифель впервые рассматривает отрицательные числа как числа, меньшие нуля (т. е. « меньшие, чем ничто »). С этого момента отрицательные числа рассматриваются уже не как долг, а совсем по-новому. Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…»
Почти одновременно со Штифелем защищал идею отрицательных чисел Бомбелли Раффаэле (около 1530—1572), итальянский математик и инженер, переоткрывший сочинение Диофанта.
Так же и Жирар считал отрицательные числа вполне допустимыми и полезными, в частности, для обозначения недостачи чего-либо.
Всякий физик постоянно имеет дело с числами: он всегда что-то измеряет, вычисляет, рассчитывает. Везде в его бумагах - числа, числа и числа. Если приглядеться к записям физика, то обнаружится, что при записи чисел он часто использует знаки "+" и "-". (Например: термометр, шкала глубин и высот)
Только в начале XIX в. теория отрицательных чисел закончила свое развитие, и "абсурдные числа" получили всеобщее признание.
Определение понятия числа
В современном мире человек постоянно пользуется числами, даже не задумываясь об их происхождении. Без знания прошлого нельзя понять настоящее. Число является одним из основных понятий математики. Понятие числа развивалось в тесной связи с изучением величин; эта связь сохраняется и теперь. Во всех разделах современной математики приходится рассматривать разные величины и пользоваться числами. Число — абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое понятие.
Существует большое количество определений понятию «число».
Первое научное определение числа дал Евклид в своих «Началах», которое он, очевидно, унаследовал от своего соотечественника Эвдокса Книдского (около 408 - около 355 гг. до н. э.): «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». Так определял понятие числа и русский математик Магницкий в своей «Арифметике» (1703 г.). Еще раньше Евклида Аристотель дал такое определение: «Число есть множество, которое измеряется с помощью единиц». В своей «Общей арифметике» (1707 г) великий английский физик, механик, астроном и математик Исаак Ньютон пишет: «Под числом мы подразумеваем не столько множество единиц, сколько абстрактное отношение какой-нибудь величины к другой величине такого же рода, взятой за единицу. Число бывает трех видов: целое, дробное и иррациональное. Целое число есть то, что измеряется единицей; дробное - кратной частью единицы, иррациональное - число, не соизмеримое с единицей».
Мариупольский математик С.Ф.Клюйков также внес свой вклад в определение понятия числа: «Числа - это математические модели реального мира, придуманные человеком для его познания». Он же внес в традиционную классификацию чисел так называемые «функциональные числа», имея в виду то, что во всем мире обычно именуют функциями.
Натуральные числа возникли при счете предметов. Об этом я узнала в 5 классе. Затем я узнала, что потребность человека измерять величины не всегда выражается целым числом. После расширения множества натуральных чисел до дробных стало возможным делить любое целое число на другое целое число (за исключением деления на нуль). Появились дробные числа. Вычитать же целое число из другого целого числа, когда вычитаемое больше уменьшаемого, долгое время казалось невозможным. Интересным для меня оказался тот факт, что долгое время многие математики не признавали отрицательных чисел, считая, что им не соответствуют какие-либо реальные явления.
Происхождение слов «плюс» и «минус»
Термины произошли от слов plus - «больше», minus - «меньше». Сначала действия обозначали первыми буквами p; m. Многие математики предпочитали или Возникновение современных знаков «+», «-» не совсем ясно. Знак «+», возможно, происходит от сокращенной записи et, т.е. «и». Впрочем, может быть он возник из торговой практики: проданные меры вина отмечались на бочке «-», а при восстановлении запаса их перечеркивали, получался знак «+».
Италии ростовщики, давая деньги в долг, ставили перед именем должника сумму долга и черточку, вроде нашего минуса, а когда должник возвращал деньги, зачеркивали ее, получалось что-то вроде нашего плюса.
Современные знаки «+» и появились в Германии в последнее десятилетие XVв. в книге Видмана, которая была руководством по счету для купцов (1489г.). Чех Ян Видман уже писал «+» и «-» для сложения и вычитания.
Чуть позднее немецкий ученый Михель Штифель написал «Полную Арифметику», которая была напечатана в 1544 году. В ней встречаются такие записи для чисел: 0-2; 0+2; 0-5; 0+7. Числа первого вида он назвал «меньше, чем ничего» или «ниже, чем ничего». Числа второго вида назвал «больше, чем ничего» или «выше, чем ничего». Вам, конечно, понятны эти названия, потому что «ничего» - это 0.
Отрицательные числа в Египте
Однако, не смотря на такие сомнения, правила действий с положительными и отрицательными числами были предложены уже в III веке в Египте. Введение отрицательных величин впервые произошло у Диофанта. Он даже использовал специальный символ для них (сейчас мы в этом качестве используем знак «минус»). Правда, ученые спорят, обозначал ли символ Диофанта именно отрицательное число или просто операцию вычитания, потому что у Диофанта отрицательные числа не встречаются изолированно, а только в виде разностей положительных; и в качестве ответов в задачах он рассматривает только рациональные положительные числа. Но в то же время Диофант употребляет такие обороты речи, как «Прибавим к обеим сторонам отрицательное», и даже формулирует правило знаков: «Отрицательное, умноженное на отрицательное, дает положительное, тогда как отрицательное, умноженное на положительное, дает отрицательное» (то, что сейчас обычно формулируют: «Минус на минус дает плюс, минус на плюс дает минус»).
(-) (-) = (+), (-) (+) = (-).
Отрицательные числа в Древней Азии
Положительные количества в китайской математике называли «чен», отрицательные - «фу»; их изображали разными цветами: «чен» - красным, «фу» - черным. Такой способ изображения использовался в Китае до середины XII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел - цифры, которые изображали отрицательные числа, перечеркивали черточкой наискось справа налево. Индийские ученые, стараясь найти и в жизни образцы такого вычитания, пришли к толкованию его с точки зрения торговых расчетов.
Если купец имеет 5000 р. и закупает товара на 3000 р., у него остается 5000 - 3000 = 2000, р. Если же он имеет 3000 р., а закупает на 5000 р., то он остается в долгу на 2000 р. В соответствии с этим считали, что здесь совершается вычитание 3000 - 5000, результатом же является число 2000 с точкой наверху, означающее «две тысячи долга».
Толкование это носило искусственный характер, купец никогда не находил сумму долга вычитанием 3000 - 5000, а всегда выполнял вычитание 5000 - 3000. Кроме того, на этой основе можно было с натяжкой объяснить лишь правила сложения и вычитания «чисел с точками», но никак нельзя было объяснить правила умножения или деления.
В V-VI столетиях отрицательные числа появляются и очень широко распространяются в индийской математике. В Индии отрицательные числа систематически использовали в основном так, как это мы делаем сейчас. Индийские математики используют отрицательные числа с VII в. н. э.: Брахмагупта сформулировал правила арифметических действий с ними. В его произведении мы читаем: « имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество - долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму».
Индийцы называли положительные числа «дхана» или «сва» (имущество), а отрицательные - «рина» или «кшайя» (долг). Впрочем, и в Индии с пониманием и принятием отрицательных чисел были проблемы.
Отрицательные числа в Европе
Не одобряли их долго и европейские математики, потому что истолкование «имущество-долг» вызывало недоумения и сомнения. В самом деле, как можно «складывать» или «вычитать» имущества и долги, какой реальный смысл может иметь «умножение» или «деление» имущества на долг? (Г.И. Глейзер, История математики в школе IV-VI классы. Москва, Просвещение, 1981)
Вот почему с большим трудом завоевали себе место в математике отрицательные числа. В Европе к идее отрицательного количества достаточно близко подошел в начале XIII столетия Леонардо Фибоначчи Пизанский, однако в явном виде отрицательные числа применил впервые в конце XV столетия французский математик Шюке. Автор рукописного трактата по арифметике и алгебре «Наука о числах в трёх частях». Символика Шюке приближается к современной (Математический энциклопедический словарь. М., Сов. энциклопедия, 1988)
Современное истолкование отрицательных чисел
В 1544 году немецкий математик Михаил Штифель впервые рассматривает отрицательные числа как числа, меньшие нуля (т. е. « меньшие, чем ничто »). С этого момента отрицательные числа рассматриваются уже не как долг, а совсем по-новому. Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…» (Г.И. Глейзер, История математики в школе IV-VI классы. Москва, Просвещение, 1981)
После этого Штифель полностью посвящает свою работу математике, в которой он был гениальным самоучкой. Один из первых в Европе после Николы Шюке начал оперировать отрицательными числами.
Знаменитый французский математик Рене Декарт в «Геометрии» (1637 год) описывает геометрическое истолкование положительных и отрицательных чисел; положительные числа изображаются на числовой оси точками, лежащими вправо от начала 0, отрицательные - влево. Геометрическое истолкование положительных и отрицательных чисел привело к более ясному пониманию природы отрицательных чисел, способствовало их признанию.
Почти одновременно со Штифелем защищал идею отрицательных чисел Р. Бомбелли Раффаэле (около 1530—1572), итальянский математик и инженер, переоткрывший сочинение Диофанта.
Бомбелли и Жирар, напротив, считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения недостачи чего-либо. Современное обозначение положительных и отрицательных чисел со знаками « + » и « - » применил немецкий математик Видман. Выражение «ниже, чем ничего» показывает, что Штифель и некоторые другие мысленно воображали положительные и отрицательные числа точками на вертикальной шкале (вроде шкалы термометра). Развитое затем математиком А. Жираром представление об отрицательных числах как о точках на некоторой прямой, располагающихся по другую сторону от нуля, чем положительные, оказалось решающим в обеспечении этим числам прав гражданства, особенно в результате развития метода координат у П. Ферма и Р. Декарта.
Вывод
В своем работе я исследовал историю возникновения отрицательных чисел. В ходе исследования я сделал вывод:
Современная наука встречается с величинами такой сложной природы, что для их изучения приходится изобретать все новые виды чисел.
При введении новых чисел большое значение имеют два обстоятельства:
а) правила действий над ними должны быть полностью определены и не вели к противоречиям;
б) новые системы чисел должны способствовать или решению новых задач, или усовершенствовать уже известные решения.
К настоящем у времени существует семь общепринятых уровней обобщения чисел: натуральные, рациональные, действительные, комплексные, векторные, матричные и трансфинитные числа. Отдельными учеными предлагается считать функции функциональными числами и расширить степень обобщения чисел до двенадцати уровней.
Все эти множества чисел я постараюсь изучить.
Приложение
СТИХОТВОРЕНИЕ
«Сложение отрицательных чисел и чисел с разными знаками»
Если уж захочется вам сложить
Числа отрицательные, нечего тужить:
Надо сумму модулей быстренько узнать,
К ней потом знак «минус» взять да приписать.
Если числа с разными знаками дадут,
Чтоб найти их сумму, все мы тут как тут.
Больший модуль быстро очень выбираем.
Из него мы меньший вычитаем.
Самое же главное - знак не позабыть!
Вы какой поставите? - мы хотим спросить
Вам секрет откроем, проще дела нет,
Знак, где модуль больше, запиши в ответ.
Правила сложения положительных и отрицательных чисел
Минус с минусом сложить,
Можно минус получить.
Если сложишь минус, плюс,
То получится конфуз?!
Знак числа ты выбирай
Что сильнее, не зевай!
Модули их отними,
Да все числа помири!
Правила умножения можно истолковать и таким образом:
«Друг моего друга - мой друг»: + ∙ + = + .
«Враг моего врага - мой друг»: ─ ∙ ─ = +.
«Друг моего врага - мой враг»: + ∙ ─ = ─.
«Враг моего друга - мой враг»: ─ ∙ + = ─.
Знак умножения есть точка, в ней три знака:
Прикрой из них два, третий даст ответ.
Например.
Как определить знак произведения 2∙(-3)?
Закроем руками знаки «плюс» и «минус». Остаётся знак «минус»
Список литературы
«История древнего мира», 5 класс. Колпаков, Селунская.
«История математики в древности», Э. Кольман.
«Справочник школьника». ИД «ВЕСЬ», Санкт-Петербург. 2003 г.
Большая математическая энциклопедия. Якушева Г.М. и др.
Вигасин А.А,.Годер Г.И., "История древнего мира" учебник 5 класса, 2001г.
Википедия. Свободная энциклопедия.
Возникновение и развитие математической науки: Кн. Для учителя. - М.: Просвещение, 1987.
Гельфман Э.Г. "Положительные и отрицательные числа", учебное пособие по математике для 6-го класса, 2001.
Глав. ред. М. Д. Аксёнова. - М.: Аванта+,1998.
Глейзер Г. И. "История математики в школе", Москва, "Просвещение", 1981 г.
Детская энциклопедия "Я познаю мир", Москва, "Просвещение", 1995г.
История математики в школе, IV-VI классы. Г.И. Глейзер, Москва, Просвещение, 1981.
М.: Филол. О-во «СЛОВО»: ОЛМА-ПРЕСС, 2005.
Малыгин К.А.
Математический энциклопедический словарь. М., Сов. энциклопедия, 1988.
Нурк Э.Р., Тельгмаа А.Э. "Математика 6 класс", Москва, "Просвещение",1989г
Учебник 5 класс. Виленкин, Жохов, Чесноков, Шварцбурд.
Фридман Л. М.. "Изучаем математику", учебное издание, 1994 г.
Э.Г. Гельфман и др., Положительные и отрицательные числа в театре Буратино. Учебное пособие по математике для 6 класса. 3-е издание, испр., - Томск: Издательство Томского университета, 1998г.
Энциклопедия для детей. Т.11. Математика
ЧИСЛО, одно из основных понятий математики; зародилось в глубокой древности и постепенно расширялось и обобщалось. В связи со счетом отдельных предметов возникло понятие о целых положительных (натуральных) числах, а затем идея о безграничности натурального ряда чисел: 1, 2, 3, 4. Задачи измерения длин, площадей и т. п. , а также выделение долей именованных величин привели к понятию рационального (дробного) числа. Понятие об отрицательных числах возникло у индийцев в 6-11 вв.
Впервые отрицательные числа встречаются в одной из книг древнекитайского трактата « Математика в девяти главах » (Джан Цань – 1 век до нашей эры). Отрицательное число понималось как долг, а положительное – как имущество. Сложение и вычитание отрицательных чисел производилось на основе рассуждений о долге. Например, правило сложения формулировалось так: « Если к одному долгу прибавить другой долг, то в результате получится долг, а не имущество ». Знака минус тогда не было, а чтобы отличать положительные и отрицательные числа, Джан Цань писал их разными по цвету чернилами.
Идея отрицательных чисел с трудом завоевывала себе место в математике. Эти числа казались математикам древности непонятными и даже ложными, действия с ними – неясными и не имеющими реального смысла.
Использование отрицательных чисел индийскими математиками.
В 6 – 7 веках нашей эры индийские математики уже систематически пользовались отрицательными числами, по-прежнему понимая их как долг. Начиная с 7 века индийские математики пользовались отрицательными числами. Положительные числа они называли « дхана » или « сва » (« имущество »), а отрицательные – « рина » или « кшайя » («долг »). Впервые все четыре арифметических действия с отрицательными числами приведены индийским математиком и астрономом Брахмагуптой (598 – 660 гг.).
Например, правило деления он формулировал так:« Положительное, делённое на положительное, или отрицательное, делённое на отрицательное, становится положительным. Но положительное, делённое на отрицательное, и отрицательное, делённое на положительное, остаётся отрицательным ».
(Брахмагупта (598 – 660 гг.) – индийский математик и астроном. До нас дошло сочинение Брахмагупта « Пересмотр системы Брахмы » (628), значительная часть, которого посвящена арифметике и алгебре. Важнейшим здесь является учение об арифметической прогрессии и решение квадратных уравнений, с которыми Брахмагупта справлялся во всех случаях, когда они имели действительные решения. Брахмагупта допускал и рассматривал употребление нуля во всех арифметических действиях. Кроме того Брахмагупта решал некоторые неопределённые уравнения в целых числах; он дал правило составления прямоугольных треугольников с рациональными сторонами и др. Брахмагупту было известно обратное тройное правило, у него встречается приближение П,самая ранняя интерполяционная формула 2 – го порядка. Его интерполяционное правило для синуса и обратного синуса при равных интервалах являются частным случаем интерполяционной формулы Ньютона – Стирлинга. В более поздней работе Брахмагупта приводит интерполяционное правило при неравных промежутках. Его работы были в 8 веке переведены на арабский язык.)
Понимание отрицательных чисел Леонардом Фибоначчи Пизанским.
Независимо от индийцев к пониманию отрицательных чисел как противоположности положительных пришёл итальянский математик Леонардо Фибоначчи Пизанский (13 в.). Но понадобилось ещё около 400 лет, прежде чем « абсурдные » (бессмысленные) отрицательные числа получили полное признание математиков, а отрицательные решения в задачах перестали отбрасываться как невозможные.
(Леонардо Фибоначчи Пизанский (ок. 1170 – после 1228) – итальянский математик. Родился в Пизе (Италия). Начальное образование получил в Буше (Алжир) под руководством местного учителя. Тут он овладел арифметикой и алгеброй арабов. Посетил многие страны Европы и Востока и всюду пополнял свои знания по математике.
Издал две книги: « Книгу об абаке » (1202), где абак рассматривался не столько как прибор, сколько, как исчисление вообще, и « Практическую геометрию » (1220). По первой книге многие поколения европейских математиков изучали индийскую позиционную систему счисления. Изложение материала в ней было оригинальным и изящным. Учёному принадлежат и собственные открытия, в частности он положил начало разработке вопросов, связанных с Т. Н. числами Фибоначчи, и дал оригинальный приём извлечения кубического корня. Его труды получили распространение только в конце 15 века, когда Лука Пачоли переработал их и опубликовал в своей книге « Сумма » .
Рассмотрение отрицательных чисел Михаилом Штифелем по - новому.
В 1544 году немецкий математик Михаил Штифель впервые рассматривает отрицательные числа как числа, меньшие нуля (т. е. « меньшие, чем ничто »). С этого момента отрицательные числа рассматриваются уже не как долг, а совсем по-новому. (Штифель Михаил (19. 04. 1487 – 19. 06. 1567) – знаменитый немецкий математик. Михаил Штифель учился в католическом монастыре, затем увлёкся идеями Лютера и стал сельским протестантским пастором. Изучая библию, старался найти в ней математическое истолкование. В результате своих изысканий предсказал конец мира на 19 октября 1533 года, который, конечно, не произошёл, а Михаил Штифель был заключён в Вюртембергскую тюрьму, из которой его вызволил сам Лютер.
После этого Штифель полностью посвящает свою работу математике, в которой он был гениальным самоучкой. Один из первых в Европе после Н. Шюке начал оперировать отрицательными числами; ввёл дробный и нулевой показатели степени, а также термин « показатель » ; в работе « Полная арифметика » (1544) дал правило деления на дробь как умножения на дробь, обратную делителю; сделал первый шаг в развитии приёмов, упрощающих вычисления с большими числами, для чего сопоставлял две прогрессии: геометрическую и арифметическую. Позднее это помогло И. Бюрги и Дж. Неперу создать логарифмические таблицы и разработать логарифмические вычисления.)
Современное истолкование отрицательных чисел Жираром и Рене Декартом.
Современное истолкование отрицательных чисел, основанное на откладывании единичных отрезков на числовой оси влево от нуля, было дано в 17 веке, в основном в работах голландского математика Жирара (1595 – 1634 гг.) и знаменитого французского математика и философа Рене Декарта (1596–1650гг.) (Жирар Альберт (1595 – 1632) – бельгийский математик. Жирар родился во Франции, но бежал в Голландию от преследований католической церкви, так как был протестантом. Альберт Жирар внёс большой вклад в развитие алгебры. Основным его сочинением была книга « Новое открытие в алгебре». Впервые высказал основную теорему алгебры о наличии корня у алгебраического уравнения с одним неизвестным. Хотя строгое доказательство впервые дал Гаусс. Жирару принадлежит вывод формулы площади сферического треугольника.) С 1629 в Нидерландах. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввел многие алгебраические обозначения. Высказал закон сохранения количества движения, дал понятие импульса силы. Автор теории, объясняющей образование и движение небесных тел вихревым движением частиц материи (вихри Декарта). Ввел представление о рефлексе (дуга Декарта). В основе философии Декарта - дуализм души и тела, «мыслящей» и «протяженной» субстанции. Материю отождествлял с протяжением (или пространством), движение сводил к перемещению тел. Общая причина движения, по Декарту, - Бог, который сотворил материю, движение и покой. Человек - связь безжизненного телесного механизма с душой, обладающей мышлением и волей. Безусловное основоположение всего знания, по Декарту, - непосредственная достоверность сознания («мыслю, следовательно, существую»). Существование Бога рассматривал как источник объективной значимости человеческого мышления. В учении о познании Декарт - родоначальник рационализма и сторонник учения о врожденных идеях. Основные сочинения: «Геометрия» (1637), «Рассуждение о методе. » (1637), «Начала философии» (1644).
ДЕКАРТ (Descartes) Рене (латинизированное - Картезий; Cartesius) (31 марта 1596, Лаэ, Турень, Франция - 11 февраля 1650, Стокгольм), французский философ, математик, физик и физиолог, основатель новоевропейского рационализма и один из влиятельнейших метафизиков Нового времени.
Жизнь и сочинения
Родившись в дворянской семье, Декарт получил хорошее образование. В 1606 году отец отправил его в иезуитскую коллегию Ла Флеш. Учитывая не очень крепкое здоровье Декарта, ему делали некоторые послабления в строгом режиме этого учебного заведения, напр. , разрешали вставать позже других. Приобретя в коллегии немало познаний, Декарт в то же время проникся антипатией к схоластической философии, которую он сохранил на всю свою жизнь.
После окончания коллегии Декарт продолжил образование. В 1616 в университете Пуатье он получил степень бакалавра права. В 1617 Декарт поступает на службу в армию и много путешествует по Европе.
1619 год в научном отношении оказался ключевым для Декарта. Именно в это время, как он сам писал в дневнике, ему открылись основания новой «удивительнейшей науки». Скорее всего, Декарт имел в виду открытие универсального научного метода, который он впоследствии плодотворно применял в самых разных дисциплинах.
В 1620-е годы Декарт знакомится с математиком М. Мерсенном, через которого он долгие годы «держал связь» со всем европейским научным сообществом.
В 1628 Декарт более чем на 15 лет обосновывается в Нидерландах, но не поселяется в каком-то одном месте, а около двух десятков раз меняет место жительства.
В 1633, узнав об осуждении церковью Галилея, Декарт отказывается от публикации натурфилософской работы «Мир», в которой излагались идеи естественного возникновения вселенной по механическим законам материи.
В 1637 на французском языке выходит работа Декарта «Рассуждение о методе», с которой, как многие считают, и началась новоевропейская философия.
В 1641 появляется главное философское сочинение Декарта «Размышления о первой философии» (на латинском языке), а в 1644 «Первоначала философии», работа, замышлявшаяся Декартом как компендий, суммирующий наиболее важные метафизические и натурфилософские теории автора.
Большое влияние на европейскую мысль оказала и последняя философская работа Декарта «Страсти души», опубликованная в 1649 г. В том же году по приглашению шведской королевы Кристины Декарт отправился в Швецию. Суровый климат и непривычный режим (королева заставляла Декарта вставать в 5 утра, чтобы давать ей уроки и выполнять другие поручения) подорвали здоровье Декарта, и, подхватив простуду, он умер от пневмонии.
Философия Декарта ярко иллюстрирует стремление европейской культуры к освобождению от старых догм и построению новой науки и самой жизни «с чистого листа». Критерием истины, считает Декарт, может быть только «естественный свет» нашего разума. Декарт не отрицает и познавательной ценности опыта, но он видит его функцию исключительно в том, чтобы он приходил на помощь разуму там, где собственных сил последнего недостаточно для познания. Размышляя над условиями достижения достоверного знания, Декарт формулирует «правила метода», с помощью которого можно прийти к истине. Первоначально мыслившиеся Декартом весьма многочисленными, в «Рассуждении о методе», они сводятся им к четырем основным положениям, составляющим «квинтэссенцию» европейского рационализма: 1) начинать с несомненного и самоочевидного, т. е. с того, противоположное чему нельзя помыслить, 2) разделять любую проблему на столько частей, сколько необходимо для ее эффективного решения, 3) начинать с простого и постепенно продвигаться к сложному, 4) постоянно перепроверять правильность умозаключений. Самоочевидное схватывается разумом в интеллектуальной интуиции, которую нельзя смешивать с чувственным наблюдением и которая дает нам «ясное и отчетливое» постижение истины. Разделение проблемы на части позволяет выявить в ней «абсолютные», т. е. самоочевидные элементы, от которых можно отталкиваться в последующих дедукциях. Дедукцией Декарт называет «движение мысли», в котором происходит сцепление интуитивных истин. Слабость человеческого интеллекта требует проверять корректность сделанных шагов на предмет отсутствия пробелов в рассуждениях. Такую проверку Декарт называет «энумерацией» или «индукцией». Итогом последовательной и разветвленной дедукции должно стать построение системы всеобщего знания, «универсальной науки». Декарт сравнивает эту науку с деревом. Корнем его является метафизика, ствол составляет физика, а плодоносные ветви образуют конкретные науки, этика, медицина и механика, приносящие непосредственную пользу. Из этой схемы видно, что залогом эффективности всех этих наук является правильная метафизика.
От метода открытия истин Декарт отличает метод изложения уже разработанного материала. Его можно излагать «аналитически» и «синтетически». Аналитический метод проблемен, он менее систематичен, но больше способствует пониманию. Синтетический, как бы «геометризирующий» материал, более строг. Декарт все же отдает предпочтение аналитическому методу.
Сомнение и несомненное
Исходной проблемой метафизики как науки о самых общих родах сущего является, как и в любых других дисциплинах, вопрос о самоочевидных основаниях. Метафизика должна начинаться с несомненной констатации какого-либо существования. Декарт «пробует» на самоочевидность тезисы о бытии мира, Бога и нашего «Я». Мир можно представить несуществующим, если вообразить, что наша жизнь есть долгое сновидение. В бытии Бога тоже можно усомниться. А вот наше «Я», считает Декарт, нельзя подвергнуть сомнению, так как само сомнение в своем бытии доказывает существование сомнения, а значит и сомневающегося Я. «Сомневаюсь, следовательно существую» - так Декарт формулирует эту важнейшую истину, обозначающую субъективистский поворот европейской философии Нового времени. В более общем виде этот тезис звучит так: «мыслю, следовательно существую» - cogito, ergo sum. Сомнение составляет лишь один из «модусов мышления», наряду с желанием, рассудочным постижением, воображением, памятью и даже ощущением. Основой мышления является сознание. Поэтому Декарт отрицает существование бессознательных идей. Мышление является неотъемлемым свойством души. Душа не может не мыслить, она - «мыслящая вещь», res cogitans. Признание несомненным тезиса о собственном существовании не означает, однако, что Декарт считает вообще невозможным несуществование души: она не может не существовать, лишь пока мыслит. В остальном же душа - случайная вещь, т. е. может как быть, так и не быть, ибо она несовершенна. Все случайные вещи черпают свое бытие извне. Декарт утверждает, что душа ежесекундно поддерживается в своем существовании Богом. Тем не менее ее можно назвать субстанцией, так как она может существовать отдельно от тела. Впрочем, на деле душа и тело тесно взаимодействуют. Однако принципиальная независимость души от тела является для Декарта залогом вероятного бессмертия души.
Учение о Боге
От философской психологии Декарт переходит к учению о Боге. Он дает несколько доказательств существования высшего существа. Наиболее известным является так называемый «онтологический аргумент»: Бог есть всесовершенное существо, поэтому в понятии о нем не может отсутствовать предикат внешнего существования, что означает невозможность отрицать бытие Бога, не впадая в противоречие. Другое доказательство, предлагаемое Декартом, более оригинально (первое было хорошо известно в средневековой философии): в нашем уме есть идея Бога, у этой идеи должна быть причина, но причиной может быть только сам Бог, так как в противном случае идея высшей реальности была бы порождена тем, что этой реальностью не обладает, т. е. в действии было бы больше реальности, чем в причине, что нелепо. Третий аргумент основан на необходимости существования Бога для поддержания человеческого существования. Декарт полагал, что Бог, не будучи сам по себе связан законами человеческой истины, является тем не менее источником «врожденного знания» человека, в которое входит сама идея Бога, а также логические и математические аксиомы. От Бога, считает Декарт, исходит и наша вера в существование внешнего материального мира. Бог не может быть обманщиком, а поэтому эта вера истинна, и материальный мир действительно существует.
Философия природы
Убедившись в существовании материального мира, Декарт приступает к исследованию его свойств. Главным свойством материальных вещей оказывается протяжение, которое может выступать в различных модификациях. Декарт отрицает существование пустого пространства на том основании, что везде, где есть протяжение, имеется и «протяженная вещь», res extensa. Другие качества материи мыслятся смутно и, возможно, считает Декарт, существуют только в восприятии, а в самих предметах отсутствуют. Материя состоит из элементов огня, воздуха и земли, все различие которых состоит только в величине. Элементы не являются неделимыми и могут превращаться друг в друга. Пытаясь согласовать концепцию дискретности материи с тезисом об отсутствии пустоты, Декарт выдвигает любопытнейший тезис о нестабильности и отсутствии определенной формы у мельчайших частиц вещества. Единственным способом передачи взаимодействий между элементами и состоящими из их смешения вещами Декарт признает соударение. Оно происходит по законам постоянства, вытекающим из неизменной сущности Бога. При отсутствии внешних воздействий вещи не меняют свое состояние и двигаются по прямой, являющейся символом постоянства. Кроме того, Декарт говорит о сохранении исходного количества движения в мире. Само движение, однако, изначально не свойственно материи, а привносится в нее Богом. Но уже одного первотолчка достаточно, чтобы из хаоса материи постепенно самостоятельно собрался правильный и гармоничный космос.
Тело и душа
Много времени Декарт уделял изучению законов функционирования животных организмов. Он считал их тонкими машинами, способными самостоятельно адаптироваться к окружающей среде и адекватно реагировать на внешние воздействия. Испытанное воздействие передается в мозг, являющийся резервуаром «животных духов», мельчайших частиц, попадание которых в мышцы через поры, открывающиеся вследствие отклонений мозговой «шишковидной железы» (являющейся седалищем души), приводит к сокращениям этих мышц. Движение тела составляется последовательностью таких сокращений. Животные лишены душ и не нуждаются в них. Декарт говорил, что его больше удивляет наличие души у человека, чем ее отсутствие у животных. Наличие души у человека, однако, не бесполезно, так как душа может корректировать естественные реакции тела.
Декарт-физиолог
Декарт изучал строение различных органов у животных, исследовал строение зародышей на различных стадиях развития. Его учение о «произвольных» и «непроизвольных» движениях заложило основы современного учения о рефлексах. В работах Декарта представлены схемы рефлекторных реакций с центростремительной и центробежной частью рефлекторной дуги.
Значение работ Декарта в математике и физике
Естественно-научные достижения Декарта родились как «побочный продукт» разрабатываемого им единыго метода единой науки. Декарту принадлежит заслуга создания современных систем обозначений: он ввел знаки переменных величин (x, y, z.), коэффициентов (a, b, c.), обозначение степеней (a2, x-1.).
Декарт является одним из авторов теории уравнений: им сформулировано правило знаков для определения числа положительных и отрицательных корней, поставил вопрос о границах действительных корней и выдвинул проблему приводимости, т. е. представления целой рациональной функции с рациональными коэффициентами в виде произведения двух функций этого рода. Он указал, что уравнение 3-й степени разрешимо в квадратных радикалах (а также указал решение с помощью циркуля и линейки, если это уравнение приводимо).
Декарт является одним из создателей аналитической геометрии (которую он разрабатывал одновременно с П. Ферма), позволявшей алгебраизировать эту науку с помощью метода координат. Предложенная им система координат получила его имя. В работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. Переменная трактуется им двояко: как отрезок переменной длины и постоянного направления (текущая координата точки, описывающей своим движением кривую) и как непрерывная числовая переменная, пробегающая совокупность чисел, выражающих этот отрезок. В область изучения геометрии Декарт включил «геометрические» линии (позднее названные Лейбницем алгебраическими) - линии, описываемые при движении шарнирными механизмами. Трансцендентные кривые (сам Декарт называет их «механическими») он исключил из своей геометрии. В связи с исследованиями линз (см. ниже) в «Геометрии» излагаются способы построения нормалей и касательных к плоским кривым.
«Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа. Действительные числа Декарт фактически трактовал как отношение любого отрезка к единичному (хотя саму формулировку дал позднее И. Ньютон). В переписке Декарта содержатся и другие его открытия.
В оптике он открыл закон преломления световых лучей на границе двух различных сред (изложены в «Диоптрике», 1637). Декарт внес серьезный вклад в физику, дав четкую формулировку закона инерции.
Влияние Декарта
Декарт оказал громадное влияние на последующую науку и философию. Европейские мыслители восприняли от него призывы к созданию философии как точной науки (Б. Спиноза), к построению метафизики на базе учения о душе (Дж. Локк, Д. Юм). Декарт активизировал и теологические споры в вопросе о возможности доказательств бытия Бога. Огромный резонанс имело обсуждение Декартом вопроса о взаимодействии души и тела, на которое откликнулись Н. Мальбранш, Г. Лейбниц и др. , а также его космогонические построения. Многие мыслители делали попытки формализовать методологию Декарта (А. Арно, Н. Николь, Б. Паскаль). В 20 веке к философии Декарта часто обращаются участники многочисленных дискуссий по проблемам философии сознания и когнитивной психологии.
Для того чтобы разработать этот понятный и естественный сейчас для нас подход, понадобились усилия многих учёных на протяжении восемнадцати веков от Джан Цаня до Декарта.
Допустим, у Дениса очень много конфет - целая большая коробка. Сперва Денис съел 3 конфеты. Потом папа дал Денису 5 конфет. Потом Денис подарил Матвею 9 конфет. Наконец, мама дала Денису 6 конфет. Вопрос: Стало ли у Дениса в конечном итоге больше или меньше конфет, чем было вначале? Если больше, то насколько больше? Если меньше, то насколько меньше?
Для того чтобы не запутаться с этой задачей, удобно применить один трюк. Давайте выпишем подряд все числа из условия. При этом мы будем ставить знак «+» перед числами, которые обозначают, насколько конфет у Дениса прибавилось, и знак «−» перед числами, которые обозначают, насколько конфет у Дениса убавилось. Тогда всё условие выпишется очень коротко:
− 3 + 5 − 9 + 6.
Эту запись можно прочитать, например, так: «Сперва Денис получил минус три конфеты. Потом плюс пять конфет. Потом минус девять конфет. И наконец плюс шесть конфет». Слово «минус» меняет смысл фразы на прямо противоположный. Когда я говорю: «Денис получил минус три конфеты», - это на самом деле означает, что у Дениса на три конфеты убыло. Слово «плюс», напротив, подтверждает смысл фразы. «Денис получил плюс пять конфет» означает то же самое, что и просто «Денис получил пять конфет».
Итак, сперва Денис получил минус три конфеты. Значит, у Дениса стало на минус три конфеты больше, чем было вначале. Для краткости можно сказать: у Дениса стало минус три конфеты.
Потом Денис получил плюс пять конфет. Легко сообразить, что у Дениса стало плюс две конфеты. Значит,
− 3 + 5 = + 2.
Потом Денис получил минус девять конфет. И вот сколько конфет у него стало:
− 3 + 5 − 9 = + 2 − 9 = − 7.
Наконец Денису досталось еще +6 конфет. И всего конфет стало:
− 3 + 5 − 9 + 6 = + 2 − 9 + 6 = − 7 + 6 = − 1.
На привычном языке это означает, что в конце концов у Дениса оказалось на одну конфету меньше, чем было вначале. Задача решена.
Трюк со знаками «+» или «−» применяется очень широко. Числа со знаком «+» называются положительными . Числа со знаком «−» называются отрицательными . Число 0 (ноль) не является ни положительным, ни отрицательным, потому что +0 ничем не отличается от −0. Таким образом, мы имеем дело с числами из ряда
..., −5, −4, −3, −2, −1, 0, +1, +2, +3, +4, +5, ...
Такие числа называются целыми числами . А те числа, у которых вообще нет никакого знака и с которыми мы имели дело до сих пор, называются натуральными числами (только ноль не относится к натуральным числам).
Целые числа можно представить себе как ступеньки лестницы. Число ноль - это лестничная площадка, находящаяся вровень с улицей. Отсюда можно ступенька за ступенькой подняться наверх, к более высоким этажам, а можно и спуститься вниз, в подвал. До тех пор, пока нам не нужно заходить в подвал, нам вполне достаточно одних только натуральных чисел и нуля. Натуральные числа - это, по сути дела, то же самое, что положительные целые числа.
Строго говоря, целое число - это не номер ступеньки, а команда на перемещение по лестнице. Например, число +3 говорит, что следует подняться на три ступеньки вверх, а число −5 означает, что надо спуститься на пять ступенек вниз. Просто за номер ступеньки принимают такую команду, которая перемещает нас на данную спупеньку, если мы начинаем движение с нулевого уровня.
Вычисления с целыми числами легко проделывать, просто мысленно прыгая вверх или вниз по ступенькам - если, конечно, не потребуется делать слишком большие прыжки. Но как быть, когда надо прыгнуть на сто или более ступенек? Ведь не будем же мы рисовать такую длиннющую лестницу!
А впрочем, почему бы и нет? Мы можем нарисовать длинную лестницу с такого большого расстояния, на котором отдельные ступеньки уже неразличимы. Тогда наша лестница превратиться просто в одну прямую линию. А чтобы ее удобнее было поместить на страницу, нарисуем ее без наклона и отдельно отметим положение ступеньки 0.
Поучимся вначале прыгать по такой прямой на примере выражений, значения которых мы уже давно умеем вычислять. Пусть требуется найти
Строго говоря, раз уж мы имеем дело с целыми числами, то нам следовало бы написать
Но у положительного числа, стоящего в начале строки знак «+» обычно не ставят. Прыжки по лестнице выглядят приблизительно так:
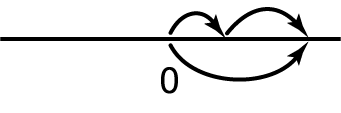
Вместо двух больших прыжков нарисованных над прямой (+42 и +53), можно сделать один прыжок, нарисованный под прямой, причем длина этого прыжка, конечно, равна
Такого рода рисуночки на математическом языке принято называть диаграммами. Вот как выглядит диаграмма для привычного нам примера на вычитание

Вначале мы сделали большой прыжок вправо, потом прыжок поменьше влево. В результате мы так и остались справа от нуля. Но возможна и другая ситуация, как, например, в случае выражения

На этот раз прыжок враво оказался короче прыжка влево: мы перелетели через ноль и оказались в «подвале» - там, где находятся ступеньки с отрицательными номерами. Вглядимся попристальнее в наш прыжок влево. Всего мы преодолели 95 ступенек. После того как мы преодолели 53 ступеньки, мы поравнялись с отметкой 0. Спрашивается сколько ступенек мы предолели после этого? Ну, конечно
Таким образом, оказавшись на ступеньке 0, мы спустились вниз еще на 42 ступеньки, а значит, в конце концов мы пришли на ступеньку с номером −42. Итак,
53 − 95 = −(95 − 53) = −42.
Подобным же образом, рисуя диаграммы, легко установить что
−42 − 53 = −(42 + 53) = −95;

−95 + 53 = −(95 − 53) = −42;

и, наконец,
−53 + 95 = 95 − 53 = 42.

Таким образом, мы научились свободно путешествовать по всей лестнице целых чисел.
Рассмотрим теперь такую задачу. Денис и Матвей обмениваются фантиками. Вначале Денис дал Матвею 3 фантика, а потом взял у него 5 фантиков. Сколько фантиков в итоге получил Матвей?
Но раз Денис получил 2 фантика, то Матвей получил −2 фантика. К прибыли Дениса мы приписали минус и получили прибыль Матвея. Наше решение можно записать в виде единственного выражения
−(−3 + 5) = −2.
Тут всё просто. Но давайте слегка видоизменим условие задачи. Пусть Денис дал сперва Матвею 5 фантиков, а потом взял у него 3 фантика. Спрашивается, опять-таки, сколько фантиков в итоге получил Матвей?
Снова вначале рассчитаем «прибыль» Дениса:
−5 + 3 = −2.
Значит, Матвей получил 2 фантика. Но как теперь наше решение записать в виде единственного выражения? Что бы такое приписать к отрицательному числу −2, чтобы получить положительное число 2? Оказывается, и на этот раз надо приписать знак минус. Математики очень любят единообразие. Они стремятся к тому, чтобы решение похожих задач записывались в виде похожих выражений. В данном случае решение выглядит так:
−(−5 + 3) = −(−2) = +2.
Так уж математики договорились: если к положительному числу приписать минус, то оно превращается в отрицательное, а если к отрицательному числу приписать минус, то оно превращается в положительное. Это очень логично. В конце концов, спуститься на минус две ступеньки вниз это то же самое, что подняться на плюс две ступеньки вверх. Итак,
−(+2) = −2;
−(−2) = +2.
Для полноты картины отметим еще, что
+(+2) = +2;
+(−2) = −2.
Это дает нам возможность по-новому взглянуть на давно привычные вещи. Пусть дано выражение
Смысл этой записи можно представлять себе по-разному. Можно, по-старинке, считать, что из положительного числа +5 отнимается положительное число +3:
В этом случае +5 называется уменьшаемым , +3 - вычитаемым , а всё выражение - разностью . Именно так учат в школе. Однако слова «уменьшаемое» и «вычитаемое» нигде, кроме школы, не употребляются и их можно забыть после итоговой контрольной работы. Про эту же самую запись можно сказать, что к положительному числу +5 прибавляется отрицательное число −3:
Числа +5 и −3 называются слагаемыми , а всё выражение - суммой . В данной сумме только два слагаемых, но, вообще, сумма может состоять из скольких угодно слагаемых. Подобным же образом, выражение
можно с одинаковым правом рассматривать как сумму двух положительных чисел:
и как разность положительного и отрицательного чисел:
(+5) − (−3).
После того как мы познакомились с целыми числами, нам обязательно надо уточнить правила раскрытия скобок. Если перед скобками стоит знак «+», то такие скобки можно просто стереть, и все числа в них сохраняют свои знаки, например:
+(+2) = +2;
+(−2) = −2;
+(−3 + 5) = −3 + 5;
+(−3 − 5) = −3 − 5;
+(5 − 3) = 5 − 3
и так далее.
Если же перед скобками стоит знак «−», то стирая скобку, мы должны также поменять знаки у всех чисел, стоявших в ней:
−(+2) = −2;
−(−2) = +2;
−(−3 + 5) = +3 − 5 = 3 − 5;
−(−3 − 5) = +3 + 5 = 3 + 5;
−(5 − 3) = −(+5 − 3) = −5 + 3;
и так далее.
При этом полезно держать в голове задачу про обмен фантиками между Денисом и Матвеем. Например, последнюю строчку можно получить так. Считаем, что Денис вначале взял 5 фантиков у Матвея, а потом еще −3. Всего Денис получил 5 − 3 фантиков, а Матвей - то же самое число, но с противоположным знаком, то есть −(5 − 3) фантиков. Но ведь эту же задачу можно решить и другим способом, имея в виду, что всякий раз, когда Денис получает, Матвей отдает. Значит, вначале Матвей получил −5 фантиков, а потом еще +3, что в итоге дает −5 + 3.
Подобно натуральным числам, целые числа можно сравнивать между собой. Зададимся, например, вопросом: какое число больше: −3 или −1? Посмотрим на лестницу с целыми числами, и сразу станет ясно, что −1 больше, чем −3, и, значит, −3 меньше, чем −1:
−1 > −3;
−3 < −1.
А теперь давайте уточним: насколько −1 больше, чем −3? Иными словами, на сколько ступенек надо подняться, чтобы перейти со ступеньки −3 на ступеньку −1? Ответ на этот вопрос можно записать в виде разности чисел −1 и −3:
− 1 − (−3) = −1 + 3 = 3 − 1 = 2.
Прыгая по ступенькам, легко проверить, что это так. А вот еще один любопытный вопрос: насколько число 3 больше числа 5? Или, что то же самое: на сколько ступенек надо подняться вверх, чтобы перейти со ступеньки 5 на ступеньку 3? Еще недавно этот вопрос поставил бы нас в тупик. Но теперь мы легко можем выписать ответ:
3 − 5 = − 2.
Действительно, если мы находимся на ступеньке 5 и поднимемся вверх еще на −2 ступеньки, то окажемся как раз на ступеньке 3.
Задачи
2.3.1. Какой смысл имеют следующие фразы?
Денис дал папе минус три конфеты.
Матвей старше Дениса на минус два года.
Чтобы попасть в нашу квартиру, надо спуститься на минус два этажа вниз.
2.3.2. Имеют ли смысл такие фразы?
У Дениса минус три конфеты.
На лугу пасется минус две коровы.
Замечание. Эта задача не имеет однозначного решения. Не будет, конечно, ошибкой утверждать, что данные высказывания бессмысленны. И в то же время им можно придать вполне ясный смысл. Допустим, у Дениса есть большая коробка, доверху наполненная конфетами, но содержимое этой коробки - не в счет. Или допустим, что две коровы из стада не вышли пастись на луг, а по какой-то причине остались в коровнике. Стоит иметь в виду, что и самые привычные фразы могут оказаться неоднозначными:
У Дениса три конфеты.
Это высказывание не исключает, что у Дениса припрятана где-то еще огромная коробка с конфетами, но о тех конфетах просто умалчивается. Точно так же, когда я говорю: «У меня пять рублей», - я не имею в виду, что это и есть всё мое состояние.
2.3.3. Кузнечик прыгает по лестнице, начиная с этажа, где находится квартира Дениса. Сначала он прыгнул на 2 ступеньки вниз, потом на 5 ступенек вверх, и наконец на 7 ступенек вниз. На сколько ступенек и в каком направлении переместился кузнечик?
2.3.4. Найти значения выражений:
− 6 + 10;
− 28 + 76;
и т.п.
− 6 + 10 = 10 − 6 = 4.
2.3.5. Найти значения выражений:
8 − 20;
34 − 98;
и т.п.
8 − 20 = − (20 − 8) = − 12.
2.3.6. Найти значения выражений:
− 4 − 13;
− 48 − 53;
и т.п.
− 4 − 13 = − (4 + 13) = − 17.
2.3.7. Для следующих выражений найти значения, проводя вычисления в том порядке, который задается скобками. Затем раскрыть скобки и убедиться, что значения выражений остались прежними. Составить задачи про конфеты, которые решаются таким образом.
25 − (−10 + 4);
25 + (− 4 + 10);
и т.п.
25 − (− 10 + 4) = 25 − (−(10 − 4)) = 25 − (−6) = 25 + 6 = 31.
25 − (− 10 + 4) = 25 + 10 − 4 = 35 − 4 = 31.
«У Дениса было 25 конфет. Он отдал папе минус десять конфет, а Матвею четыре конфеты. Сколько конфет у него стало?»
Чалина Ирина
Презентация об истории возникновения отрицательных чисел.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Отрицательные числа Чалина Ирина
Математика – виват! Слава, слава, слава! Не поют ей серенад, Не кричат ей браво. Жили-были 2 числа, Жили, не тужили. Один – минус, другой – плюс, Весело дружили. Знаки разные во всем, Но поставить можно, Чтоб сложилося число, Которое быть должно. Плюс на плюс – получим плюс, Плюс на минус – будет минус. Ну а если (-20) прибавим (-8), То в итоге мы получим число (-28).
Отрицательное число Отрица́тельное число́ - элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля. Все отрицательные числа, и только они, меньше, чем нуль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Историческая справка История говорит о том, что люди долго не могли привыкнуть к отрицательным числам. Отрицательные числа казались им непонятными, ими не пользовались, просто не видели в них смысла. Положительные числа трактовали как «прибыль», а отрицательные – как «долг», «убыток». В Древнем Египт е, Вавилон е и Древней Греции не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Но знаков + или – в древности не было ни для чисел, ни для действий. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены. Греки тоже поначалу знаки не использовали, пока Диофант Александрийский в III веке стал использовать знак « - » при решении линейных уравнений. Знак « + » появился как результат противоположного действия знаку « - » путем перечеркивания минуса. Было очень похоже на тот плюс, который мы используем сейчас. Он уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.
Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта (VII век) уже рассматривал их наравне с положительными. В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Даже Паскаль считал, что 0 − 4 = 0, так как ничто не может быть меньше, чем ничто. Бомбелли и Жирар, напротив, считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения недостачи чего-либо. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия. В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 - в ней первый член слева больше второго, а справа - наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии. Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке Уильямом Гамильтоном и Германом Грассманом.
Свойства отрицательных чисел Отрицательные числа подчиняются практически тем же алгебраическим правилам, что и натуральные, но имеют некоторые особенности. Если любое множество положительных чисел ограничено снизу, то любое множество отрицательных чисел ограничено сверху. При умножении целых чисел действует правило знаков: произведение чисел с разными знаками отрицательно, с одинаковыми - положительно. При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на обратный. Например, умножая неравенство 3 −10. При делении с остатком частное может иметь любой знак, но остаток, по соглашению, всегда неотрицателен (иначе он определяется не однозначно). Для каждого натурального числа (n) существует одно и только одно отрицательное число, обозначаемое (-n), которое дополняет n до нуля: Оба числа называются противоположными друг для друга. Вычитание целого числа (a) из другого целого числа (b) равносильно сложению b с противоположным для a знаком: (b)+ (-а)
Основные правила Правило 1. Сумма двух отрицательных чисел есть число отрицательное, равное сумме модулей этих чисел. Пример - Сумма чисел (-3) и (-8) равно минус 11. Правило 2 . Произведение двух чисел с разными знаками есть отрицательное число, модуль которого равен произведению модулей сомножителей. Пример - Произведение минус трех и пяти равно минус пятнадцати, потому что при умножении двух чисел с разными знаками получается отрицательное число, а его модуль равен произведению модулей сомножителей, то есть трех и пяти. Правило 3 . Чтобы отметить отрицательные числа, надо координатный луч дополнить противоположным ему лучом и нанести на него соответствующие координаты. Пример. Числа, расположенные на координатной прямой справа от нуля, называются положительными, а слева – отрицательными.
Модуль отрицательного числа Расстояние от точки А(а) до начала отсчета, т.е. до точки О(о), называют модулем числа а и обозначают /а/ Модуль отрицательного числа равен числу, ему противоположному. Модуль, ничего не делая с положительными числами и нулем, отнимает у отрицательных чисел знак "минус". Модуль обозначается вертикальными черточками, которые пишутся с двух сторон от числа. Например / -3 / = 3; / -2,3 / = 2,3 ; / -526/7 / = 526/7. Из двух отрицательных чисел больше то, модуль которого меньше и, меньше то, модуль которого больше. (По этому поводу обычно шутят, что у отрицательных чисел все не как у людей, наоборот)
вывод Отрицательные числа в наши дни вещь обыденная: их используют, например, для того, чтобы представить температуру ниже нуля. Поэтому кажется удивительным, что еще несколько столетий назад какой-либо конкретной интерпретации отрицательных чисел не было, а возникающие по ходу вычислений отрицательные числа назывались «воображаемыми». Отрицательные числа нужны не только при измерении температуры. Например, если предприятие получило доход на 1 млн.руб., или, наоборот, потерпело убытки на 1 млн.руб., как это отразить в финансовых документах? В первом случае записывают 1000 000 руб. или + 1000000 руб. А во втором, соответственно, (- 1 000 000 руб.).
Спасибо за внимание! -